PHYSIQUE  II

De la généralisation à toute interaction de cette formule, on déduit la loi de Newton pour deux corps de masses M et m :

f = - K mM/r²

La constante K est appelée constante de gravitation. Elle a pour dimension M^-1L³T^-2 et pour valeur :

6,67 x 10^-11 unités S.I.

On a posé k = 4p²a³/T² = KM. Les mesures T, a et K permettent donc de déterminer la masse du soleil.
Si a (demi-grand axe de l'orbite) et T (période de révolution) sont relatives au mouvement d'une planète de masse m autour du soleil, et si a' et T' sont les grandeurs correspondantes pour le mouvement d'un satellite autour de la planète, on obtient en divisant membre à membre l'égalité suivante :

k / k' = M / m  =  a³ / T²  x  T'² / a'³

^{Cette relation permet de connaître la masse des planètes lorsque l'on connaît la masse du soleil, et d'en déduire par le même calcul la masse de ses satellites.}

ÉQUATION DE LA TRAJECTOIRE 

On utilise directement la formule de Binet :

f = - K mM/r² = - m (C² / r²) ( d²u/dQ²  + u ) avec u = 1 / r ce qui donne l'équation différencielle de la trajectoire :

d²u / dQ²  + u  =  K  M / C²

Il s'agit d'une équation différentielle du second ordre à coefficients constants avec second membre. La solution en est :

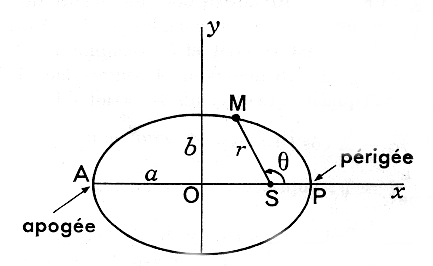
r = p / ( 1 + e cos (Q - a))

avec p = C² / KM = C² / k et e = Ap
La trajectoire est donc une conique pour laquelle a est l'angle que fait l'axe focal avec l'axe des coordonnées polaires.

ENERGIE TOTALE DU MOBILE

L' énergie totale du mobile W est la somme de son énergie potentielle et de son énergie cinétique.
Il est démontré que V = - K (Mm)/r

W = 1 / 2 m [ (C² / r⁴) (dr / dQ)² + C² / r² ] - KMm / r  =  1 / 2 mC² [ (du / dQ)² + u² ] - KMmu

en posant u = - 1/r. Or on sait que u = K M / C² + A cos(Q - a) et du / dQ = -A sin (Q - a), d'où, en remplaçant dans l'expression de W :

W = 1/2 mC² [A² - (KM/C²)²] et en exprimant les constantes C et A en fonction de p et e :

W = 1/2 KM m ((e² -1) / p)

Or p est toujours positif, mais e est inférieur à 1 pour une trajectoire elliptique, égal à 1 pour une trajectoire parabolique et supérieur à 1 pour une trajectoire hyperbolique. Donc :

a- Si l'énergie totale constante est négative, la trajectoire est une ellipse (e < 1).

Lorsque le mobile décrit sa trajectoire, l'énergie cinétique croît et l'énergie potentielle diminue, et vice versa, de telle sorte que leur somme reste constante.
L'énergie cinétique est maximale (et l'énergie potentielle minimale) lorsque le mobile passe au périgée P, la distance r étant alors minimale : r_p=a(1-e).
L'énergie cinétique est minimale (et l'énergie potentielle maximale) lorsque le mobile passe à l'apogée A, la distance r étant alors maximale : r_a= a(1+e).

b- Si l'énergie totale constante est nulle, la trajectoire est une parabole (e = 1).

c- SI l'énergie totale constante est positive, la trajectoire est une hyperbole (e > 1).

L'énergie cinétique croît, passe par un maximum lorsque la distance r est minimale (r=a=c/e) et décroît ensuite.

VITESSE DE LIBÉRATION

La vitesse de libération est la vitesse au dessus de laquelle un engin lancé d'un astre s'en éloigne indéfiniment.
On considère une planète comme formée de couches concentriques homogènes. Il résulte alors du théorème de Gauss appliqué au champ newtonien que le champ de gravitation est le même que s'il était crée par une masse ponctuelle située au centre de la planète et de même masse M.
Cette approximation est applicable aux satellites de forme sphérique, dans lesquels la matière est généralement organisés en couches concentriques.
D'autre part, d'après le théorème du mouvement du centre d'inertie, le mouvement du centre d'inertie d'un engin lancé d'un astre est celui d'un point matériel de masse m égale à celle de l'engin.

Si l'engin est lancé avec un vitesse v_o d'un point situé à une distance r_o du centre de l'astre, il possèdera une énergie totale W qui restera constante si on fait abstraction de la résistance d'une éventuelle atmosphère, et on a :

W = 1/2 mv²_o - K Mm/r_o

Si W=0, la trajectoire est parabolique; si W>0, la trajectoire est hyperbolique. Dans les deux cas, l'engin s'éloignera indéfiniment.

Donc, W >= 0  c'est à dire  v_o >= (2KM/r_o)^1/2

On appelle vitesse de libération v_l la vitesse limite inférieure de v_o pour que l'engin s'éloigne indéfiniment.

v_l = (2KM/r_o)^1/2

Cette vitesse de libération, indiquée lorsqu'elle est significative dans le tableau détaillé des satellites, est très importante pour déterminer à priori l'existence d'une atmosphère sur un astre. Les molécules de gaz ont en effet une vitesse moyenne fonction de leur composition et de la température. Certains satellites sont trop petits pour retenir une quelconque atmosphère.